Number System Class 9th NCERT Maths

We have provided you with the notes of Number Systems Class 9th Maths along with the mind map of Number systems class 10th maths to help the students better understand the Class 9th Maths Chapter 1 Number Systems.

We have also shared NCERT Solutions For Class 9th Maths Chapter 1 Number Systems to help the students to give the best solutions of the chapter Number Systems to boost their confidence regarding the solutions and improve their accuracy.

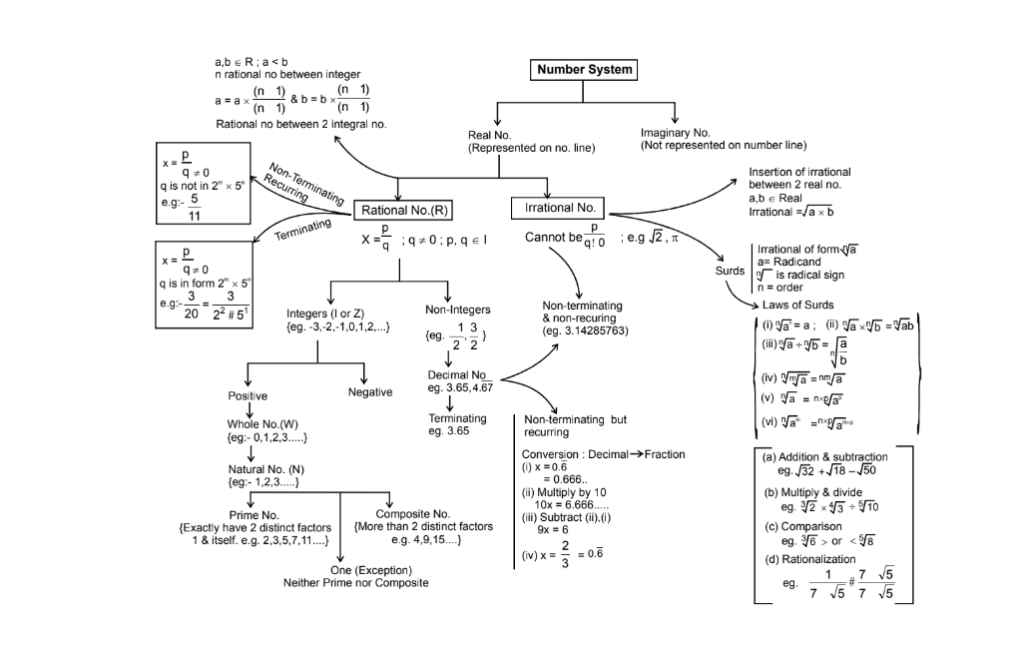
Number Systems Class 9th Maths: Mind Map

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems

Here we are providing you with the Number Systems class 9th Ncert Maths Solutions to help you gain confidence in solutions and get a better understanding of the lesson.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.1

Ex 1.1 Class 9 Maths Question 1.
Is zero a rational number? Can you write it in the form pq,where p and q are integers and q ≠0?
Solution:
Yes, zero is a rational number it can be written in the form pq.
0 = 01 = 02 = 03 etc. denominator q can also be taken as negative integer.

Ex 1.1 Class 9 Maths Question 2.
Find six rational numbers between 3 and 4.
Solution:
Let q_i be the rational number between 3
and 4, where j = 1 to 6.
∴ Six rational numbers are as follows:

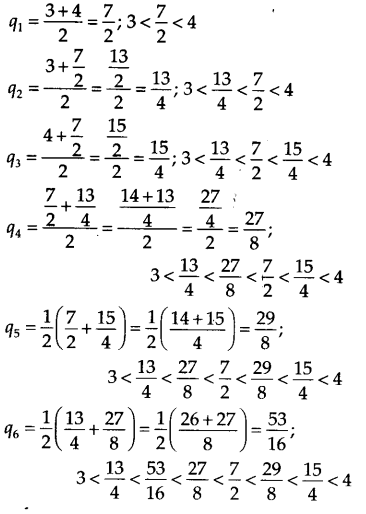
Thus, the six rational numbers between 3 and 4 are

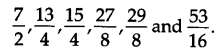
Ex 1.1 Class 9 Maths Question 3.
Find five rational numbers between 35 and 45.
Solution:
Since, we need to find five rational numbers, therefore, multiply numerator and denominator by 6.

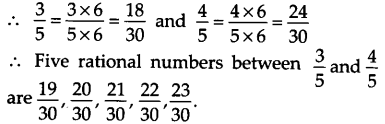
Ex 1.1 Class 9 Maths Question 4.
State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
Solution:
(i) True
∵ The collection of all natural numbers and 0 is called whole numbers.
(ii) False
∵ Negative integers are not whole numbers.
(iii) False
∵ Rational numbers are of the form p/q, q ≠ 0 and q does not divide p completely that are not whole numbers.

Ex 1.2 Class 9 Maths Question 2.
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Solution:
No, if we take a positive integer, say 9, its square root is 3, which is a rational number.

Ex 1.2 Class 9 Maths Question 3.
Show how √5 can be represented on the number line.
Solution:
Draw a number line and take point O and A on it such that OA = 1 unit. Draw BA ⊥ OA as BA = 1 unit. Join OB = √2 units.
Now draw BB₁ ⊥ OB such that BB₁ =1 unit. Join OB₁ = √3 units.
Next, draw B₁B₂⊥ OB₁such that B₁B₂ = 1 unit.
Join OB₂ = units.
Again draw B₂B₃ ⊥OB₂ such that B₂B₃ = 1 unit.
Join OB₃ = √5 units.

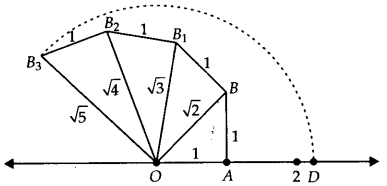
Take O as centre and OB₃ as radius, draw an arc which cuts the number line at D.
Point D
represents √5 on the number line.

Ex 1.2 Class 9 Maths Question 4.
Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP₁, of unit lengths Draw a line segment P₁, P₂ perpendicular to OP₁ of unit length (see figure). Now, draw a line segment P₂P₃ perpendicular to OP₂. Then draw a line segment P₃P₄ perpendicular to OP₃. Continuing in this manner, you can get the line segment P_n-1 P_n by drawing a line segment of unit length perpendicular to OP_{n – 1}. In this manner, you will have created the points P₂, P₃,…… P_n,….. and joined them to create a beautiful spiral depicting √2,√3,√4,……

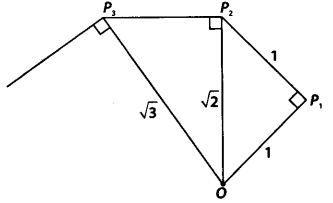
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3

Ex 1.3 Class 9 Maths Question 1.
Write the following in decimal form and say what kind of decimal expansion each has

Solution:
(i) We have, 36100 = 0.36
Thus, the decimal expansion of 36100 is terminating.

(ii) Dividing 1 by 11, we have

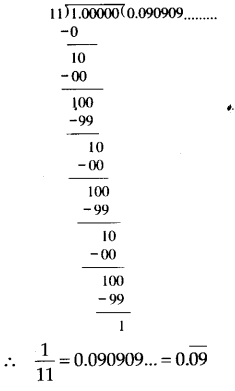
Thus, the decimal expansion of 111 is non-terminating repeating.

(iii) We have, 418 = 338
Dividing 33 by 8, we get

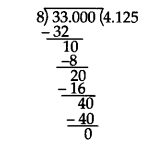
∴ 418 = 4.125. Thus, the decimal expansion of 418 is terminating.

(iv) Dividing 3 by 13, we get

Here, the repeating block of digits is 230769
∴ 313 = 0.23076923… = 0.230769¯
Thus, the decimal expansion of 313 is non-terminating repeating.

(v) Dividing 2 by 11, we get

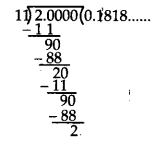
Here, the repeating block of digits is 18.
∴ 211 = 0.1818… = 0.18¯
Thus, the decimal expansion of 211 is non-terminating repeating.

(vi) Dividing 329 by 400, we get

Ex 1.3 Class 9 Maths Question 2.
You know that 17 = 0.142857¯. Can you predict what the decimal expansions of 27 , 137 , 47 , 57 , 67 are , without actually doing the long division? If so, how?
Solution:
We are given that 17 = 0.142857¯.
∴ 27 = 2 x 17 = 2 x (0.142857¯) =0.285714¯
37 = 3 x 17 = 3 x (0.142857¯) = 0.428571¯
47 = 4 x 17 = 4 x (0.142857¯) = 0.571428¯
57 = 5 x 17 = 5 x(0.142857¯) = 0.714285¯
67 = 6 x 17 = 6 x (0.142857¯) = 0.857142¯
Thus, without actually doing the long division we can predict the decimal expansions of the given rational numbers.

Ex 1.3 Class 9 Maths Question 3.
Express the following in the form pq where p and q are integers and q ≠ 0.
(i) 0.6¯
(ii) 0.47¯
(iii) 0.001¯¯¯¯¯¯¯¯
Solution:
(i) Let x = 0.6¯ = 0.6666… … (1)
As there is only one repeating digit,
multiplying (1) by 10 on both sides, we get
10x = 6.6666… … (2)
Subtracting (1) from (2), we get
10x – x = 6.6666… -0.6666…
⇒ 9x = 6 ⇒ x = 69 = 23
Thus, 0.6¯ = 23

(ii) Let x = 0.47¯ = 0.4777… … (1)
As there is only one repeating digit, multiplying (1) by lo on both sides, we get
10x = 4.777
Subtracting (1) from (2), we get
10x – x = 4.777…… – 0.4777…….
⇒ 9x = 4.3 ⇒ x = 4390
Thus, 0.47¯ = 4390

(iii) Let x = 0.001¯¯¯¯¯¯¯¯ = 0.001001… … (1)
As there are 3 repeating digits,
multiplying (1) by 1000 on both sides, we get
1000x = 1.001001 … (2)
Subtracting (1) from (2), we get
1000x – x = (1.001…) – (0.001…)
⇒ 999x = 1 ⇒ x = 1999
Thus, 0.001¯¯¯¯¯¯¯¯ = 1999

Ex 1.3 Class 9 Maths Question 4.
Express 0.99999… in the form pqAre, you surprised by your answer? With your teacher and classmates, discuss why the answer makes sense.
Solution:
Let x = 0.99999….. …. (i)
As there is only one repeating digit,
multiplying (i) by 10 on both sides, we get
10x = 9.9999 … (ii)
Subtracting (i) from (ii), we get
10x – x = (99999 ) — (0.9999 )
⇒ 9x = 9 ⇒ x = 99 = 1
Thus, 0.9999 =1
As 0.9999… goes on forever, there is no such a big difference between 1 and 0.9999
Hence, both are equal.

Ex 1.3 Class 9 Maths Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 117? Perform the division to check your answer.
Solution:
In 117, In the divisor is 17.
Since the number of entries in the repeating block of digits is less than the divisor, the maximum number of digits in the repeating block is 16.
Dividing 1 by 17, we have

The remainder I is the same digit from which we started the division.
∴ 117 = 0.0588235294117647¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Thus, there are 16 digits in the repeating block in the decimal expansion of 117.
Hence, our answer is verified.

Ex 1.3 Class 9 Maths Question 6.
Look at several examples of rational numbers in the form pq (q ≠ 0). Where p and q are integers with no common factors other than 1 and have terminating decimal representations (expansions). Can you guess what property q must satisfy?
Solution:
Let us look at the decimal expansion of the following terminating rational numbers:

We observe that the prime factorisation of q (i.e. denominator) has only powers of 2 or powers of 5 or powers of both.

Ex 1.3 Class 9 Maths Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Solution:
√2 = 1.414213562 ………..
√3 = 1.732050808 …….
√5 = 2.23606797 …….

Ex 1.3 Class 9 Maths Question 8.
Find three different irrational numbers between the rational numbers 57 and 911 .
Solution:
We have,

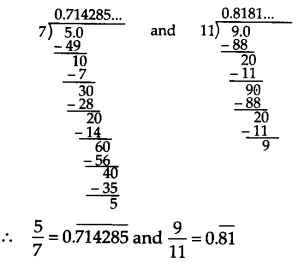
Three irrational numbers between 0.714285¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ and 0.81¯¯¯¯¯ are
(i) 0.750750075000 …..
(ii) 0.767076700767000 ……
(iii) 0.78080078008000 ……

Ex 1.3 Class 9 Maths Question 9.
Classify the following numbers as rational or irrational
(i) 23−−√
(ii) 225−−−√
(iii) 0.3796
(iv) 7.478478…..
(v) 1.101001000100001………
Solution:
(1) ∵ 23 is not a perfect square.
∴ 23−−√ is an irrational number.
(ii) ∵ 225 = 15 x 15 = 15²
∴ 225 is a perfect square.
Thus, 225−−−√ is a rational number.
(iii) ∵ 0.3796 is a terminating decimal.
∴ It is a rational number.
(iv) 7.478478… = 7.478¯¯¯¯¯¯¯¯
Since, 7.478¯¯¯¯¯¯¯¯ is a non-terminating recurring (repeating) decimal.
∴ It is a rational number.
(v) Since, 1.101001000100001… is a non terminating, non-repeating decimal number.
∴ It is an irrational number.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.4

Ex 1.4 Class 9 Maths Question 1.
Visualize 3.765 on the number line using successive magnification.
Solution:
3.765 lies between 3 and 4.

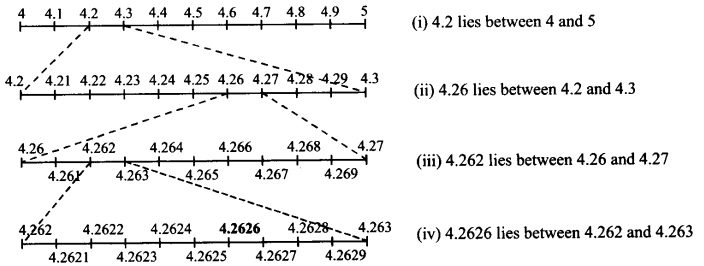
Ex 1.4 Class 9 Maths Question 2.
Visualize 4.26¯ on the number line, up to 4 decimal places.
Solution:
4.26¯ or 4.2626 lies between 4 and 5.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5

Ex 1.5 Class 9 Maths Question 1.
Classify the following numbers as rational or irrational.

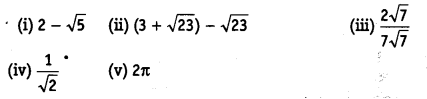
Solution:
(i) Since, it is a difference of a rational and an irrational number.
∴ 2 – √5 is an irrational number.
(ii) 3 + 23−−√ – 23−−√ = 3 + 23−−√ – 23−−√ = 3
which is a rational number.
(iii) Since, 27√77√ = 2×7√7×7√ = 27 , which is a rational number.
(iv) ∵ The quotient of rational and irrational number is an irrational number.
∴ 12√ is an irrational number.
(v) ∵ 2π = 2 x π = Product of a rational and an irrational number is an irrational number.
∴ 2π is an irrational number.

Ex 1.5 Class 9 Maths Question 2.
Simplify each of the following expressions

Solution:
(i) (3 + √3)(2 + √2)
= 2(3 + √3) + √2(3 + √3)
= 6 + 2√3 + 3√2 + √6
Thus, (3 + √3)(2 + √2) = 6 + 2√3 + 3√2 + √6
(ii) (3 + √3)(3 – √3) = (3)² – (√3)²
= 9 – 3 = 6
Thus, (3 + √3)(3 – √3) = 6
(iii) (√5 + √2)² = (√5)² + (√2)² + 2(√5)(√2)
= 5 + 2 + 2√10 = 7 + 2√10
Thus, (√5 + √2 )² = 7 + 2√10
(iv) (√5 – √2)(√5 + √2) = (√5)² – (√2)² = 5 – 2 = 3
Thus, (√5 – √2) (√5 + √2) = 3

Ex 1.5 Class 9 Maths Question 3.
Recall, π is the ratio of a circle’s circumference (say c) to its diameter (say d). That is π = cd. This seems to contradict the fact that n is irrational. How will you resolve this contradiction?
Solution:
When we measure the length of a line with a scale or with any other device, we only get an approximate national value, i.e. c and d are irrational.
∴ cd is irrational, and hence π is irrational.
Thus, there is no contradiction in saying that it is irrational.

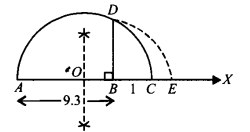
Ex 1.5 Class 9 Maths Question 4.
Represent 9.3−−−√ on the number line.
Solution:
Draw a line segment AB = 9.3 units and extend it to C such that BC = 1 unit.
Find the midpoint of AC and mark it as O.
Draw a semicircle taking O as center and AO as radius. Draw BD ⊥ AC.
Draw an arc taking B as center and BD as radius, meeting AC produced at E such that BE = BD = 9.3−−−√ units.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.6

Ex 1.6 Class 9 Maths Question 1.
Find:

Solution:
(i) 64 = 8 x 8 = 8²
∴ (64)^1/2 = (82)^1/2 = 8^{2 x 1/2} = 8 [(a^m)ⁿ = a^{m x n}] (ii) 32 = 2 x 2x 2 x 2 x 2 = 2⁵
∴ (32)^1/5= (2⁵)^1/5= 2^{5 x 1/5} = 2 [(a^m)ⁿ= a^{m x n}] (iii) 125 = 5 x 5 x 5 = 5³
∴ (125)^1/3 = (5³)^1/3 = 5^{3 x 1/3} = 5 [(a^m)ⁿ = a^{m x n}]

Ex 1.6 Class 9 Maths Question 2.
Find:

Solution:
(i) 9 = 3 x 3 = 3²
∴ (9)^3/2= (3²)^3/2 = 3^{2 x 3/2} = 3³ = 27
[(a^m)ⁿ = a^mn] (ii) 32 = 2 x 2 x 2 x 2 x 2= 2⁵
∴ (32)^2/5 = (2⁵)^2/5 = 2^{5 x 2/5} = 2² = 4
[(a^m)ⁿ = a^mn] (iii) 16 = 2 x 2 x 2 x 2 = 2⁴
∴ (16)^3/4 = (2⁴)^3/4 = 2^{4 x 3/4} = 2³ = 8
[(a^m)ⁿ = a^mn] (iv) 125 = 5 x 5 x 5 = 53
∴ (125)^-1/3 = (5³)^-1/3 = 5^{3 x (-1/3)} = 5^-1
= 15 [ a^-n 1an ]

Ex 1.6 Class 9 Maths Question 3.
Simplify:

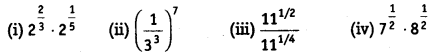
Solution:
(i) 2^2/3. 2^1/5 = 2^{2/3 + 1/5} = 2^13/15
[a^m. aⁿ = a^{m + n}

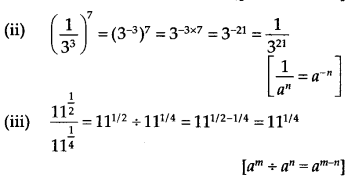
Conclusion

We have shared the notes of Number Systems Class 9th Maths along with the mind map of Number systems class 10th maths to help the students better understand the Class 9th Maths Chapter 1 Number Systems. We have shared the notes to reduce the fear and anxiety of mathematics among children of class 9th. Class 9th mathematics is very important for them, and we have provided everything per the new CBSE syllabus.

Related Articles